I’ve been in a little bit of a black hole for the last month. Work in financial tech has really ramped up to another level. One coding binge lasted 14 days straight before a major release. Do I regret it? Not at all! The work is creative, and I’m developing a system that continues to work and complete tasks while I sleep. It’s incredibly rewarding. I’ve also been developing data pipelines which take data or some form in (usually a database call). This data then goes through a series of steps in order to change and shape the data to something that’s needed for the analysis or view.

So what’s prompted this post? Data points. There have been multiple times where I have been working with people who do not code, who have struggled with why something’s the case because they don’t understand data points. This is a shame because their background knowledge of the situation is a great attribute to the analysis of the data. Here are 5 basic concepts about data points that will help you apply your background knowledge of the field to data analysis and processing.

Binary outcomes 

This is the simplest of the simplest. In order for a variable to have an effect on a machine learning algorithm, it has to have a weight. This is also true for traditional statistical analysis. The basic premise is to assign a one or zero to an outcome that could be true or false. Generally, most programming languages will have a True False concept in their syntax. True is usually denoted as a one, and False denoted by a zero. Therefore when you’re classifying your binary outcomes, True should always be one, and False should be zero. If we left the outcome as a word, it would not be able to be weighted, as you cannot multiply a word by a number. The weight value is the effect that the outcome has if the outcome is positive. If it’s negative, then it’s zero as multiplying a weight by zero is zero.

Multiple classifications 

Sometimes your data point will have multiple outcomes for one field. A classic example of this is the gender of the patient/customer. For this example we have a gender column, this comprises of Male, Female, or not specified. For this you create three new columns:

We don’t add the Not Specified column because if the person is a not specified, they will be negative for male and female. A machine learning algorithm will be able to classify this, and if a simple lookup is needed, if the person is negative for both, then the function can return not specified. This removes the need for a whole column and reduces the dimensionality for training a machine learning algorithm, speeding up the training. This is known as “one hot encoding” or “getting dummies”. In many packages, there is an option to drop one of the columns.

Numerical 

This is a standard number. These don’t need any processing to be weighted. However, there can be a lot of variance. This can be reduced by “standardizing” the data. This is usually scaled between 0-1 by the following:

(V – min V)/(max V – min V)

There are other techniques for standardization with different pros and cons.

Binning 

This is where we get numerical data and put it into groups depending on the range. These groups are known as bins. A classic example I come across a lot of the time is heart rate. Many people who know the field, but are not familiar with how data can be processed like to exclude heart rate as a predictive variable. Their objection is that there’s too much variance. For instance, clinically, I wouldn’t worry too much if a patient’s heart rate was 70, and it was 80 before. However, it would alter the outcome due to the weighting. This may uncover, a finer relationship between the outcome and the heart rate that humans are not aware of but due to the random nature of these fluctuations, it’s not likely. Binning is another way of dealing with this. If the heart rate is below 50, it goes into one bin, if it’s between 50-100 it goes into another bin, and if it’s over 100, it goes into another bin. These bins could be assigned the values, one, two, and three. Or they could be binary outcomes like the one hot encoding. There’s no reason why you can’t try both approaches to see which one has the best outcome.

Rate of Change 

To me, this is an important factor that can really flip an analysis on its head. Sadly, it’s not practiced much. This is measured by taking two reference points on the X-axis. The rate of change is calculated by dividing the change between X by the change in Y. Why is this important? Well anyone who knows me at all knows that I hate one-dimensional statistics, and the rate of change can really punch a hole in misleading one-dimensional statistics. A great example that I’ve used before is the effect of armed homicides that gun buyback in Australia had. After the gun buyback, there were fewer homicides. This is the backbone of smug social media posts and simplistic newspaper articles:

“And today, there is a wide consensus that our 1996 reforms not only reduced the gun-related homicide rate, but also the suicide rate. The Australian Institute of Criminology found that gun-related murders and suicides fell sharply after 1996.”

However, if we are looking at time-sensitive data, the rate of change before and after needs to be taken into account:

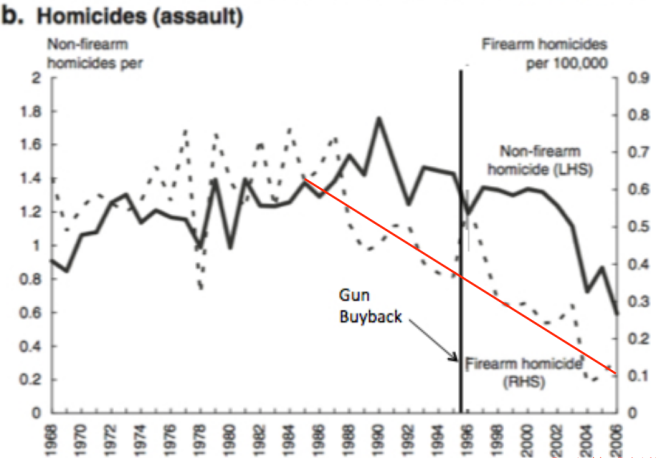
As you can see, ten years before the gun buyback, the armed homicide rate was declining, and it continued to decline at the same rate of change. With many trading algorithms, there is a point X in the past to the present reading where the rate of change is calculated in order to help predict the future. However, you have to be careful. As you can see from the graph above, if we waited a few years after, the starting point would be higher, meaning that we could claim that the gun buyback slowed the reduction of homicide. If we would wait even more and have our starting point in one of the two troughs, we could claim that the homicide reduction was increased by the buyback. What I’ve done when drawing the line is have an equal distribution of 10 years either side.

Another metric is comparing rates of change. For instance, we can look at the comparison of unarmed robbery to armed robbery in Australia:

If we look at equal ranges of the gun buyback, the rate of change of armed homicides increased. In the early 2000s policing was increased to fight this upward trend. As we can see, unarmed is reducing a lot quicker. The main argument for people fighting against gun control is that the criminals don’t adhere to the law, leaving only law-abiding citizens disarming themselves. On the other hand, people are concerned with the ease that mentally ill people can get guns. …… I’m going to be honest, I flip regularly on the gun control debate. Anyone who claims that it’s simple, hasn’t really read up on the situation. But mainly, I hope this section demonstrates the extra level of analysis that the rate of change brings. This can be done by going back a defined number of data points, then calculating the rate of change, and adding this to the current data point. Comparisons would be calculating both rates of changes, and minus one from the other.